집합론은 어떤 수학인가?

 

모든 자연의 언어는 수학으로 적습니다

수학의 언어는 먼저 '수론'과 '집합론'으로 적고 표현합니다

오랫만에 일본어로 된 집합론 책을 구입했습니다

 

집합론은 쉬워보여도 수학과에서 한 학기동안 꼭 배웁니다

-물론 중고등학교에서 배웁니다-

나중에 깊이 들어가면 심오하고 어렵습니다

 

이 집합론은 수학적일뿐만 아니라

매우 철학적입니다

이 집합론은 원래 독일의 칸토르와 데데킨트에서 유래합니다

 

 

 

이 일본어로 된 집합론 책은 배송료를 포함하여 3만5천원입니다 10일만에 옵니다

주로 우크라이나 수학자 '베른슈타인 정리'때문에 구입합니다

정통파는 독일어로 된 책을 읽습니다 저도 가능하지만 다음에 읽기를 바랍니다

 

 

 

제가 러시아어를 프랑스어로 번역한 함수해석학 책(A.N. Kolmogorov)을 보다가

'칸토르-베른슈타인의 정리'를 보고서 처음으로 집합론을 다시 보기로 했습니다

집합론은 수학뿐만 아니라 저의 철학의 수립에도 반드시 중요합니다

 

소박한 집합론 즉 원소 집합 부분집합 그 집합의 연산 그리고 비로소 나오는

'집합의 집합' = 집합족 그리고 부분집합의 집합으로 위상수학이 나옵니다

그러나 집합론(集合論)의 모순과 '공리적 집합론'은 인류의 지성의 큰 영광입니다

 

세계적 A급 현대수학자 다비트 힐버트(David Hilbert)는 이렇게 말했습니다

'그 누구도 칸토르가 창조한 (집합론의) 낙원에서 우리를 추방시킬 수 없다'고 했습니다

누구라도 집합론을 공부하면 여러가지 면에서 새로운 사람이 됩니다!

 

(*집합 = Menge, Ensemble, Set, Мно́жество, 集合입니다*)

 

 

A와 B의 교집합의 여집합입니다

처음보는 집합의 연산입니다(러시아의 위키백과)

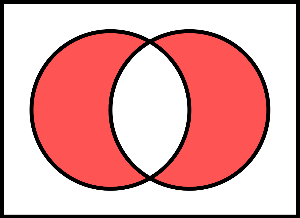
이른바 대칭차(對稱差)의 집합입니다